Non-equilibrium systems exhibit a wide variety of behaviors, including bifurcations where their properties change dramatically. Despite this variety, a large part of the observed behavior can be understood using methods from dynamical systems and nonlinear physics.
A few examples are described below.

Instabilities of ensemble of grains interacting at long distance

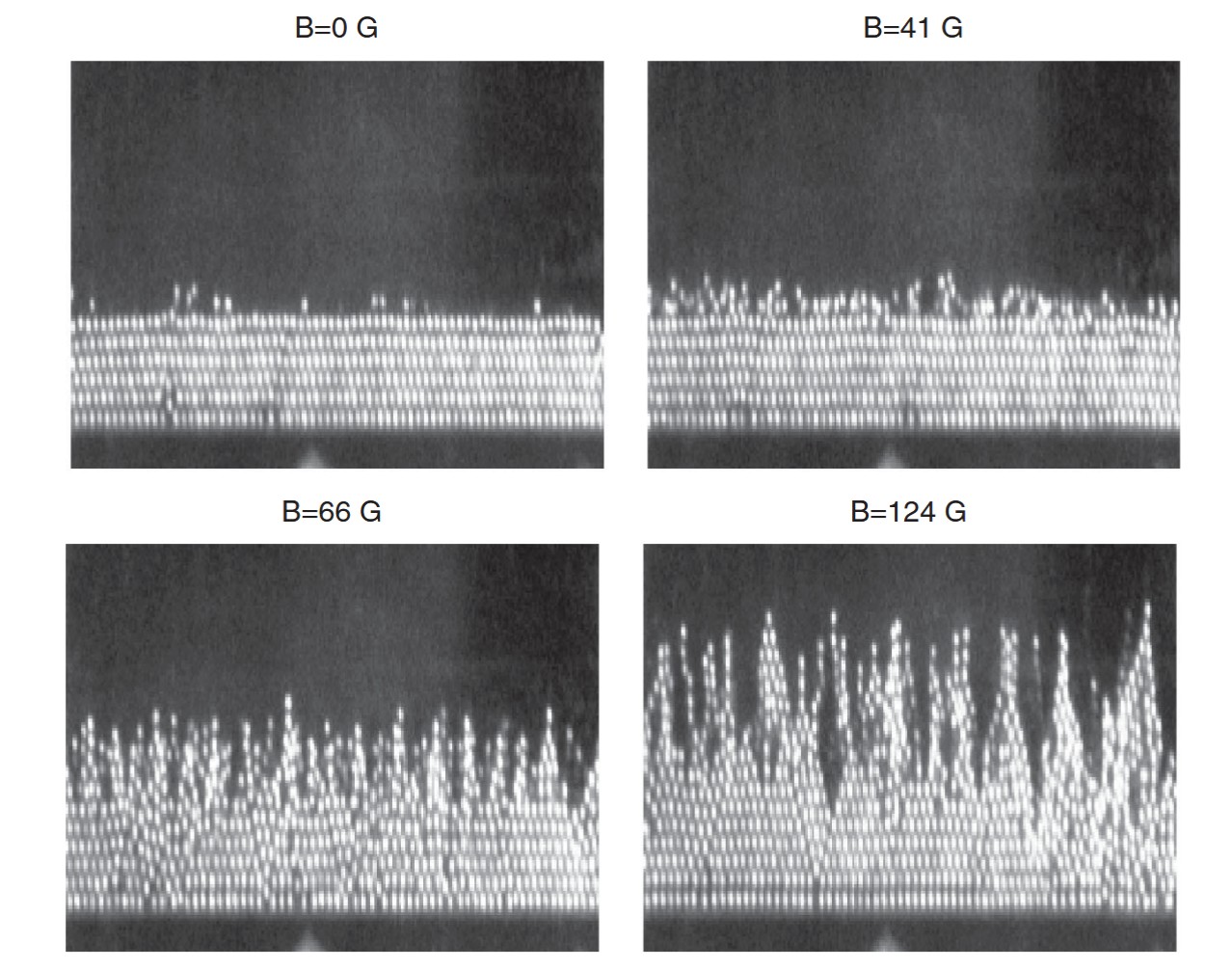
Steel grains can be magnetized when plunged in a magnetic field and then interact at large distance. We observed several new instabilities such as a peak forming instability similar to the Rosensweig instability of ferrofluids or a condensation from a low dense phase to a dense solid like phase.

rosen — Evolution of a granular layer plunged in a vertical magnetic field and subject to a moderate vertical shaking. Peaks appear above a critical magnetic field.

Observation of the condensation of a gas of interacting grains
C. Laroche, F. Pétrélis
European Physical Journal B (77) 489-492 (2010)

Surface instability driven by dipole-dipole interactions in a granular layer
Lopez D, Pétrélis F
Physical Review Letters, (104) 158001 (2010)

Oscillatory instability of interacting grains in a turbulent flow
Gallet B, Pétrélis F
Europhysics Letters (87) 54004 (2009)

Chaotic motors

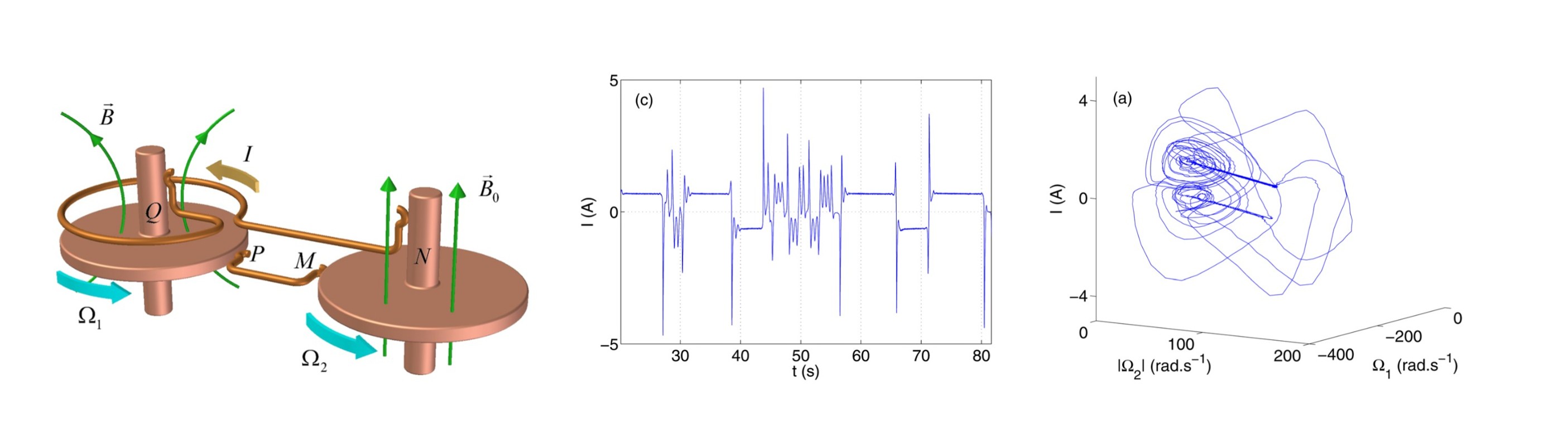
Universal motors can be used either as a usual motor when current is injected in its coils or as a current generator by dynamo instability if it is put into rotation.
When a motor is used as a generator and drives a second motor, the system displays several bifurcations such as a standard pitchfork bifurcation or a Hopf bifurcation.
Above the onsets of these bifuractions, a chaotic dynamic is possible which results from Silnikov’s mechanism of chaos.

Chaotic motors
C. Laroche, R. Labbé, F. Pétrélis, S. Fauve
American Journal of Physics (80), 113-121 (2012)

Quasi biennal oscillation

The quasi-biennial oscillation is a periodic change in the direction of winds in the Earth stratosphere. With a period slightly larger than two years, the wind direction reverses and this occurs all around the Earth. The mechanism responsible for the formation of the wind relies on internal waves that propagate in density-stratified medium, such as the stratosphere. 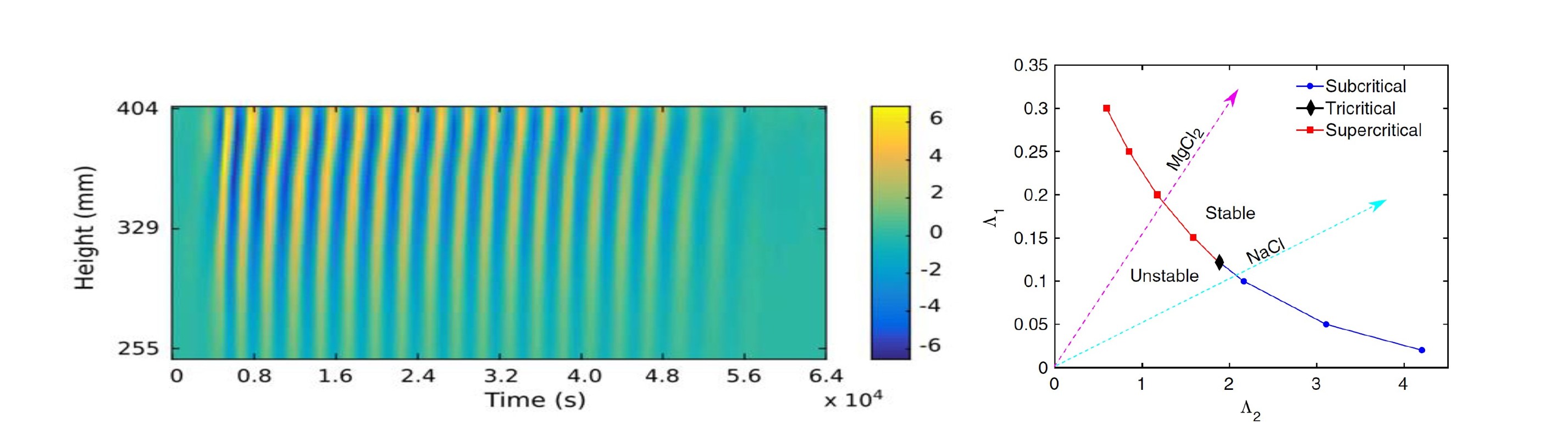Nonlinear effects cause energy transfer from the waves to the large-scale mode (with zero wave vector and frequency). In some cases, a large-scale flow appears. With B. Semin and S. Fauve, we conducted an experimental study on the interaction of internal waves with a large-scale flow and observed the analogous to the QBO: the large scale flow reverses periodically, with a period much larger than that of the internal waves. We could understand the nature of the bifurcation and its non linear regimes. In particular bistability can occur.

Observation of the instability and description of its nonlinear regime

QBO — (Left) Velocity of the mean flow as a function of time and vertical position. Note the periodic reversals and the propagation of the sign change. (Right) Parameter space and onset of instabilities.

Selected publications

Quasi-biennial oscillation: laboratory experiments
B. Semin, F. Pétrélis,
Comptes Rendus. Physique,1-25 (2024)

Nonlinear saturation of the large scale flow in a laboratory model of the quasibiennial oscillation
B. Semin, N. Garroum, F. Pétrélis, and S. Fauve
Physical Review Letters (121), 134502 (2018)

Waves and patterns

On the scattering of sound by a magnetic field in a MHD fluid
Pétrélis F, Lund F
European Physical Journal B 35 (3), 291-294 (2003)

Tidal conversion at a submarine ridge
Pétrélis F, Llewellyn Smith SL , Young WR
Journal of Physical Oceanography 36 (6), 1053-1071 (2006)

Drifting patterns as field reversals
F. Pétrélis, C. Laroche, B. Gallet, S. Fauve
Europhysics Letters (112), 54007 (2015)

Acoustic Measurement of Surface Wave Damping by a Meniscus
G. Michel, F. Pétrélis, S. Fauve
Physical Review Letters, (116), 174301 (2016)

Observation of nonlinear sloshing induced by wetting dynamics
G. Michel, F. Pétrélis, S. Fauve
Physical Review Fluids, (2), 022801 (2017)