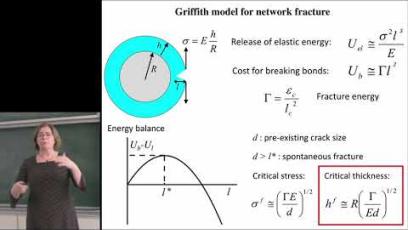
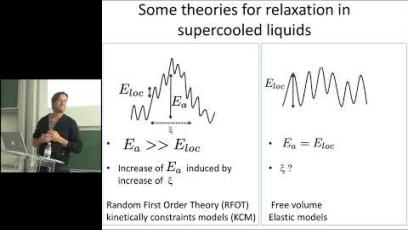
Image


Composé de 460 personnes dont 120 chercheurs/enseignants-chercheurs, le département de Physique est la plus grande structure de recherche et d’enseignement de l’ENS.
Il occupe 12 000 m² d’un bâtiment historique de la rue Lhomond, sur le campus de l’ENS à Paris, 2 000 m² sur le campus de Jussieu et quelques bâtiments au Collège de France.