
Welcome
Introduction
Links and Refs
Standard Model
Accelerators
Relativity
Nobel Prizes
String Theory
Unification
Extra dimensions
Sociology
Duality
Internet
Branes
Duality
Black holes
M-Theory
Reactions
I. Introduction
We formulate a few ideas that underlie the whole text. Firstly, we mention the use of mathematics and how we intend to avoid it and secondly, we describe why we immediately jump into explaining cutting edge physics, instead of backtracking the history of the subject. Moreover, we give the reader an idea of where the text is headed, and how the different chapters fit into the whole. Readers that don't like introductions are invited to immediately jump to chapter II.
Natural language
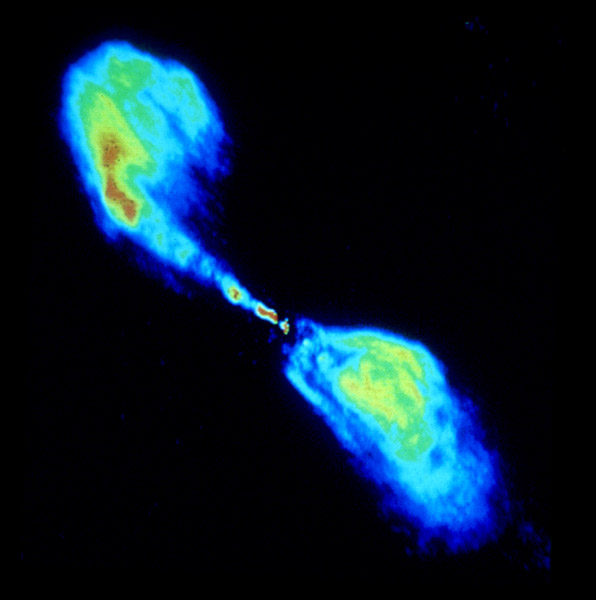 Long time ago, the Egyptians,
the Mesopotamian's and the Old Chinese tried to describe the natural world
that surrounded them accurately, and presumably the people that came before
them too, felt the same urge when confronted with the cycle of the seasons,
or the changing positions of the stars in the sky. The systematic study
of nature was carried further in the age of the Greeks, and at the same
time they developed a better sense for abstract mathematics. And it turned
out that the development of mathematics helped to describe natural phenomena
more accurately.
Long time ago, the Egyptians,
the Mesopotamian's and the Old Chinese tried to describe the natural world
that surrounded them accurately, and presumably the people that came before
them too, felt the same urge when confronted with the cycle of the seasons,
or the changing positions of the stars in the sky. The systematic study
of nature was carried further in the age of the Greeks, and at the same
time they developed a better sense for abstract mathematics. And it turned
out that the development of mathematics helped to describe natural phenomena
more accurately.
The Greek Pythagoras, for instance, was able to use abstract but simple
mathematics to describe a natural phenomenon very precisely. He discovered
the fractions that govern the harmonious musical notes. For example, a
stretched string on a cello that produces a C note when you strike it,
will give a C an octave higher when you divide its length by two. (Similarly,
when we cut of a quarter of the length of the original string, the new
string will sound like an F note) This is a famous early example of the
use of mathematics to describe a physical phenomenon accurately. Pythagoras
used the mathematics of fractions to describe the frequency of musical
notes. In the ages that followed, of Galileo, Kepler, Newton and Einstein,
mathematics became the prime language to depict nature. The mathematics
of numbers, sets, functions, surfaces etcetera turned out to be the most
useful tool for those people that felt the urge to understand the laws
governing nature. 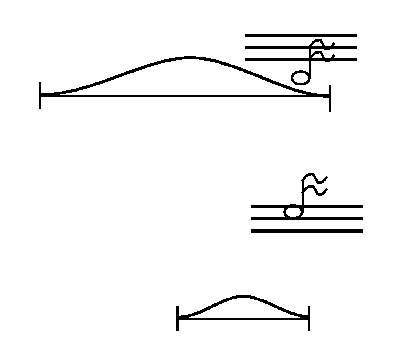
Don't panic !
The natural language in which we express the laws of nature remains the language of mathematics to this day, and the more the theories of physics evolved, the more abstract and intricate the mathematics became. That is no reason to panic and assume that without a thorough knowledge of mathematics one cannot grasp beautiful physical ideas, as we will argue shortly.It is the job of physicists to understand the theories that fit the behavior of the natural world in all their details, and if necessary, to find new theories to describe new phenomena, or to invent theories that predict effects that have never been seen before. A physicist a priori doesn't care whether his description is one in words, or one in formulas. But the history of physics taught present-day physicists that mathematics is a language well-suited for their job, and that theories expressed in formulas turned out to be more useful, accurate and economic than theories expressed in long essays. It is understandable then that most physicists know their mathematics well, and that most new physical theories are expressed in mathematical formulas. How can somebody with no mathematical background at all understand cutting edge physics then ?
 Luckily, the gist
of many mathematical ideas can be expressed in words or pictures -- we
might loose some of the accuracy of our description, but hardly the excitement
or beauty of the ideas otherwise hidden in a deep forest of formulas.
And it is often only the beauty and excitement of new insights that most
people are interested in. They want to know what new conceptual insights
have been gained the last years; they do not want to be buried under a
pile of technical details.
Luckily, the gist
of many mathematical ideas can be expressed in words or pictures -- we
might loose some of the accuracy of our description, but hardly the excitement
or beauty of the ideas otherwise hidden in a deep forest of formulas.
And it is often only the beauty and excitement of new insights that most
people are interested in. They want to know what new conceptual insights
have been gained the last years; they do not want to be buried under a
pile of technical details.
A better argument still for pictures and words, is that a lot of mathematics first originated in figures, or in ideas first formulated in plain English. Especially the mathematics needed in the physical description of nature turns out to be well-suited for drawing corresponding comprehensible pictures that capture most of the mathematics that underlie them -- after all we can for instance draw the orbits of the planets, or the paths of stars in the sky on a piece of paper, and most people will be able to understand from a picture how the planets move around the sun in ellipses. Plain English too can be used to convey a lot of physics. Indeed, professional physicists will often talk over the phone in almost ordinary English to communicate their ideas to each other -- and it often turns out to be extremely useful for them too to state their ideas in words, as it will be for us.
While always keeping in the back of our minds the more accurate, technically elaborate mathematical formulation of physical theories, it is our intention to let as many people as possible penetrate into the most complex and beautiful physical theory that exists at this moment, simply by making use of pictures, and plain words. The few formulas that we will use should be seen as merely more pictorial aides complementing the explanatory sentences in the body of the text, and the many ordinary figures.
Accumulation
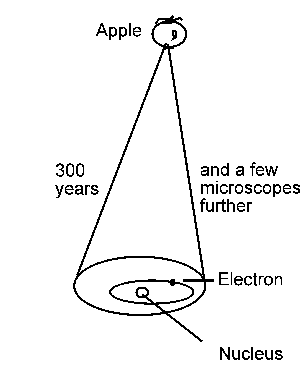 When a physicist
argues that physics is cumulative, his main point is that the description
wo/man has developed of the natural phenomena that surround her have become
more and more accurate over the ages. Newton's laws described the motion
of massive bodies better than Galileo's ideas, and Einstein's theory of
special relativity added even more accuracy to Newton's laws, as we will
recall in our chapter on general relativity. Indeed, the predictions that
old physicists were able to make on the motion of the planets, have never
been lost. We are not merely able to make the same predictions, and check
them again, we are capable now of making much more detailed forecasts. The
shift in world view that we made when we went from the idea of Ptolemy that
the earth was in the center of the universe, to the Copernican view of the
sun as the center of our solar system may look spectacular -- the most important
gain we drew from it is that the second perspective allowed us (in the end)
to find more accurate descriptions of the planetary motions.
When a physicist
argues that physics is cumulative, his main point is that the description
wo/man has developed of the natural phenomena that surround her have become
more and more accurate over the ages. Newton's laws described the motion
of massive bodies better than Galileo's ideas, and Einstein's theory of
special relativity added even more accuracy to Newton's laws, as we will
recall in our chapter on general relativity. Indeed, the predictions that
old physicists were able to make on the motion of the planets, have never
been lost. We are not merely able to make the same predictions, and check
them again, we are capable now of making much more detailed forecasts. The
shift in world view that we made when we went from the idea of Ptolemy that
the earth was in the center of the universe, to the Copernican view of the
sun as the center of our solar system may look spectacular -- the most important
gain we drew from it is that the second perspective allowed us (in the end)
to find more accurate descriptions of the planetary motions.
Some predictions of old theories we lose when replacing them by new theories, namely those that were never checked and moreover would have turned out to be false when checked. A new and better theory should make more and more accurate predictions than an old one. In that sense the predictive power of physics has steadily grown over centuries and centuries, despite recent claims from outside the scientific community to the contrary.
It is not my intention to follow the historical development of physics from its earliest day, to its present state. Since it is one of my goals to convey to you our knowledge of the natural world, and since our theories are largely cumulative, I merely need to introduce the most accurate descriptions of nature that we have come up with so far. It is already a sufficient task to describe the most salient aspects of these theories, without having to go through a historical reconstruction of these theories. (Of course, a historical reconstruction would be fascinating material in its own right.)
These most accurate theories developed hitherto are the Standard Model, treated in detail in chapter II, and General Relativity, explained in chapter III. These two theories describe almost all natural phenomena that we have observed to this day amazingly well. They have been verified in thousands of contrived experiments and are very widely accepted as the best physical theories that wo/man has invented so far.
It is my intention in these two chapters to recall the salient features of these two beautiful theories in a concise and understandable manner. Moreover, I will give leads into the vast body of literature for the layman that has accumulated around these two subjects that will guide the reader most interested in these particular sub domains of physics. My aim in this book is to press on to more recent subjects, less extensively treated in the literature. I will start realizing this goal in the first chapter on String Theory, chapter IV.
Leaps of faith
 From chapter IV onwards, you will have to take several leaps of faith with
me. We will boldly go where no wo/man has gone before. I will point out
the well-known shortcomings of the Standard Model and Einstein's theory
of General Relativity, and will argue for a theory that on the one hand
resolves these problems, and on the other hand unifies the two theories.
The model of nature that accomplishes this tour de force, is String Theory.
Moreover, it is the only model up to date that does so, after decades of
trial and error in model building, by thousands of physicists.
From chapter IV onwards, you will have to take several leaps of faith with
me. We will boldly go where no wo/man has gone before. I will point out
the well-known shortcomings of the Standard Model and Einstein's theory
of General Relativity, and will argue for a theory that on the one hand
resolves these problems, and on the other hand unifies the two theories.
The model of nature that accomplishes this tour de force, is String Theory.
Moreover, it is the only model up to date that does so, after decades of
trial and error in model building, by thousands of physicists.
No wonder String Theory is an amazingly complex mathematical construct, with miraculous physical effects hidden deep inside the guts of its formulas. As we will see in chapter IV, it is a huge tree of a theory, with branches sprouting in many different directions, having unforeseen consequences for modern mathematics as well as for other branches of physics.
Unfortunately, to this day, following me into chapter IV, String Theory, and onward, indeed still requires a leap of faith. Although there are extremely strong theoretical reasons to doubt the Standard Model and the theory of General Relativity, there are no clear cut experiments yet that contradict them, nor are there experiments that verify predictions made by String Theory. Nevertheless, the technical and theoretical arguments for String Theory seem so strong to me, that I have no trouble taking the leap. I hope to convince you that you can take a look at the far future of physics if you follow me.
And the future of physics looks bright. Indeed, the new phenomena predicted by String Theory are so dazzling that I will only treat the most important among them, and devote a chapter to each of them, specifically, to Extra Dimensions in chapter V, to Duality in chapter VI, and to Branes in chapter VII. Chapter VIII is devoted to one of the most spectacular theoretical advances made in String Theory. String Theory turns out to provide an explanation to one of the most elusive properties of black holes, namely their entropy.
Beyond String Theory
Only in the last chapter will I fulfil the promise made in the title. A last leap of faith will be necessary to enter the realm of M-theory in chapter IX. Indeed, once again we find that the theory we have just constructed, String Theory, is not complete as yet, for theoretical, but nevertheless convincing, reasons. That leads us to postulate the existence of M-theory, of which many properties are known, but for which a full formulation does not exist to this moment. The whole community of String Theorists would be very happy if somebody came along and explained to them in mathematical terms the mysterious and magical M-theory. In chapter IX, I explain some of its mysterious properties, and indicate the reasons why it is the contemporary Holy Grail for string theorists.Intermezzo's
In between some later chapters, I will insert descriptions of the present day structure of scientific research in the high-energy community. I hope these short stories about the tools, the relations, the travels, the seminars and the conferences of string theorists, as well as descriptions of the lives of the people who do research in the field will help to close the gap between laymen and women, and the cliche image of the dull and mad scientist, with wild hair and his or her tongue stuck out. Enjoy.