
Welcome
Introduction
Links and Refs
Standard Model
Accelerators
Relativity
Nobel Prizes
String Theory
Unification
Extra dimensions
Sociology
Internet
Branes
Duality
Black holes
M-Theory
Reactions
Mail me
VI. Duality
Duality
The idea of duality is not too difficult to understand, although there are very non-trivial applications. The idea of duality refers to the possibility that there might be two descriptions for the same thing. It is quite obvious that this occurs often. The two descriptions might be very easily related, as in the following example. Suppose we specify the location of a point by giving its (x,y,z) coordinates. Suppose now I have the same space, but choose a different coordinate system. The same point will now have (x',y',z') coordinates. The two descriptions of the location of the point are obviously equivalent (and easily related).
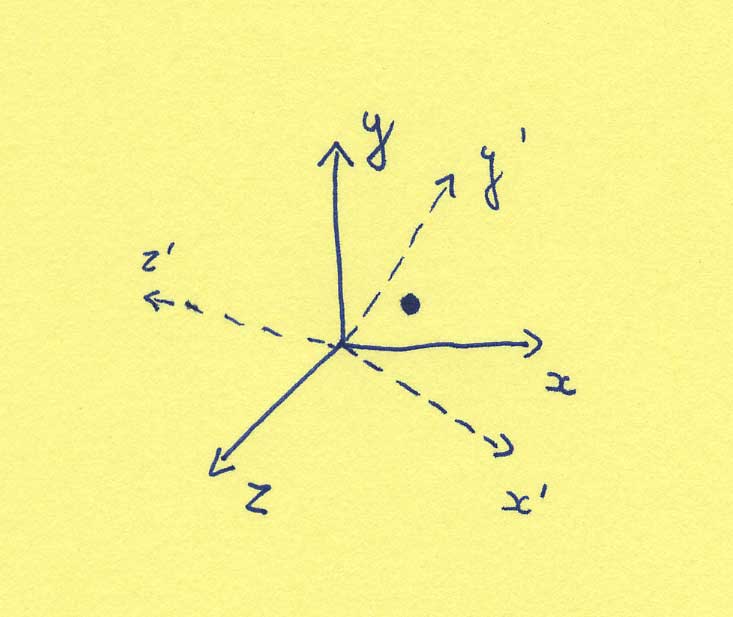
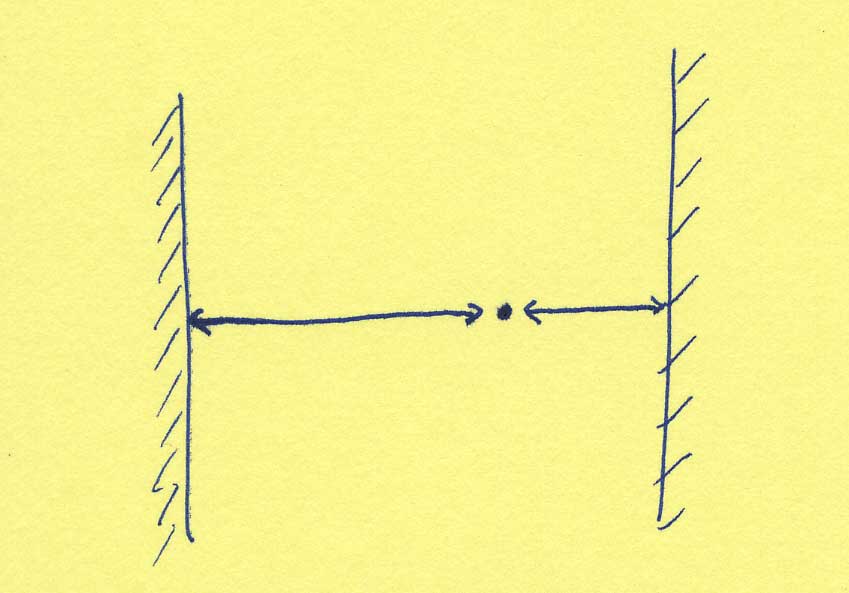
(A more concrete example would be given by assuming, for instance that the room we're in is 10 meters wide and that we say that a shoe is 4 meters from the left wall. We could as well have said that it is 6 meters from the right wall.)
There are however much less trivial examples of the idea of duality. Sometimes one can describe the same phenomena in a different way and not even realize it. It is not difficult to think of an example of this in real life either, by giving a crazy description of an everyday object, say in terms of all its constituent atoms. Would you be able to tell whether it was a chair or a table by looking at such a lengthy description ?
In some cases it involves a deep insight into two seemingly distinct physical theories to realize that they are actually descriptions of the same physics. Such theories are said to be dual, and there will be a map from the one physical theory to the other, making clear that the description of a phenomenon in one theory actually has an equivalent but seemingly different description in the dual theory. We will discuss two examples of this phenomenon that are important in string theory, although the idea of duality is prominent in many other areas of physics too.
T-duality
(Warning: technical section.)
The first example of two dual string theories are a theory of closed strings that has one dimension which is precisely like a circle. If you wish, you may imagine this circle to be a fifth dimension of space-time (on top of our time-dimension, as well as our three space dimensions). Let's say the circle of the fifth dimension has a radius length R, or in other words, the length of the extra dimension is 2 Pi R. Let's call this string theory "theory A". Let's imagine we have a second string theory, "theory B", that is precisely like the previous one, except that the fifth dimension on which it lives has a radius which is 1/RT where T is a parameter, which is equal to the tension of the string, and where R is the radius of the circle of theory A. These two string theories, theory A and theory B are dual, i.e. they have precisely the same physical content. This statement is deep, and we will give only a few plausibility arguments for the fact that it is true. Then we will hurry on to draw spectacular conclusions from it.
How could it be that string theory is equivalent on a large or on a small circle ? We'll have a look at the different forms a string can take when living in string theory A or string theory B, and we will find a one-to-one map between the shapes (=forms, o more technically, "states") in one theory to the states in the other theory. We will look at two different types of states.
First, consider the extremely small strings that just look like points on the circle. They behave like point-particles on the circle. Point-particles, when considered quantum mechanically, behave like waves. For a wave to be able to live on a circle, it has to form such a pattern that it closes on itself. The wavelength has to be a fraction of the length of the circle. That is equivalent (via the deBroglie relation), to saying that the momentum has to be a multiple of the inverse of the radius of the circle. Thus, there are string states with momentum or mass n/R for theory A (with n integer), and there are string states with mass m/(1/R.T)=m R.T for theory B (with m integer). (If you have never heard of wave-functions, de Broglie, and periodic functions before reading this site, it is high time for you to move on to a less technical section or to start a long search for these concepts on the internet.)
Next, we look at the strings that wind around the circle. Since these are closed strings, they have to wind around the circle an integer number of times. But because the strings have a certain tension, it takes some energy or mass for them to stretch over the circle. The mass of these strings is proportional to their tension, and to the number of times they wind around the circle. For theory A, they have a mass kR.T, while for theory B they have a mass q.(1/RT).T=q/R (with both k and q generic integers).
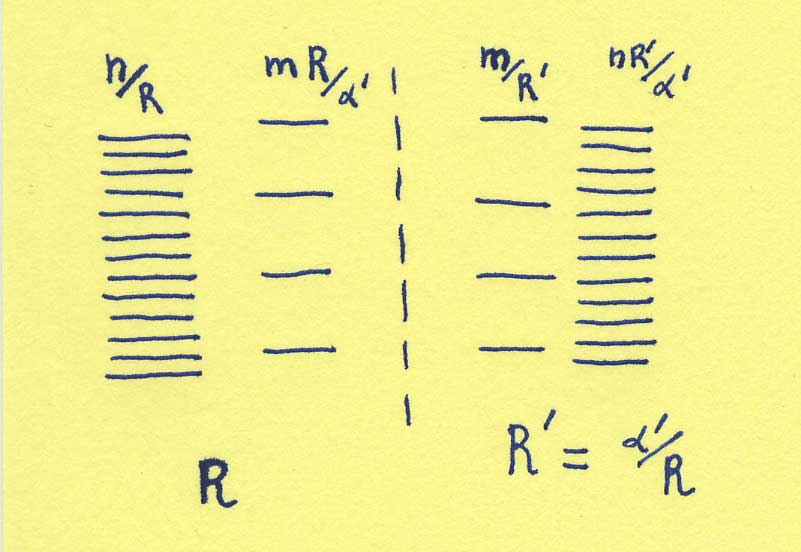
We understood part of the states for closed strings of theory A on a circle of radius R, and theory B on a circle of radius 1/RT. And miraculously, it turns out that there is a one-to-one map. Indeed, the particle like states in theory A with mass n/R can be mapped onto the stretching strings of theory B with mass q/R (when we map the state with momentum n to the state winding q times). Similarly, the winding states of theory A can be mapped to the particle like states of theory B.
Note that this miracle could never happen in a theory of particles. We would only find the particle like states in both theory A and B, and we would never find a duality between the two theories.
The only thing we showed up until now is the nice map between certain states of theory A and theory B. It turns out that this map can be completed for all the states in theory A and theory B, and moreover, that the state of theory A behaves exactly the same in theory A as its image behaves in theory B. That is a second miracle.
This indicates that we have found a duality between two theories. What do we learn from such a duality ? Although this example sounded fairly trivial, we can draw mind boggling conclusions from it. Indeed, we can infer from this example a smallest distance in the universe we studied. Indeed, since a string theory on a circle of radius R is equivalent to a string theory on a circle of radius 1/RT we can do the following. Once we want to study a string theory A on a circle of radius R smaller than (1/T)^{1/2} (i.e. the square root of the inverse of the string tension), we might as well study string theory B on a circle of radius 1/RT bigger than (1/T)^{1/2}. In other words, we never need to study a string theory of radius smaller than (1/T)^{1/2}! If we try to make the radius even smaller, we just won't see the difference between that theory, and the theory with bigger radius. That is spectacular typically stringy phenomenon.
The example we discussed is a simple instance of a very large class of dualities between large and small compact spaces, between straight and tilted spaces, and between very complicated spaces and other very complicated spaces. One of the nice spin-offs of string theory lies exactly in these dualities. Since string theory on space A depends on the precise properties of space A, and similarly for space B, there will be a map between certain properties of space A and B, once we know that there is a stringy T-duality between string theory on space A and B.
Thus stringy T-duality allows us to study properties of a complicated space A, by scrutinizing other, perhaps more manageable properties of space B. This has fascinated mathematicians called algebraic geometers, because by studying string theory they could finally solve some geometrical problems on complicated spaces by using stringy T-duality, or so-called mirror symmetry. By scrutinizing a manageable property of space B, and using the mirror duality map, they could find properties of space A that they had been after for decades.
Another, more physical consequence of stringy T-duality is that it supports the idea that the big bang, i.e. the birth of the universe out of a singular point in space-time is presumably a very naive picture of the history of our universe. That is not to say that we need to rewrite early cosmology, but just that we can presumably get a less singular and more satisfying picture of what went on at extremely early times by studying consequences of a theory of quantum gravity. Indeed, if universes of very small size look equivalent to universes of bigger sizes, we may be able to get a better intuition for physics at the big bang. (This is a very naive description of advanced present day research in the field.)
S-duality
In the previous sections on T-duality we already saw examples of how a duality could allow us to examine properties of a theory that would otherwise be very difficult to access. S-duality is another duality that allows for such a drastic simplification. Indeed, we already saw that string theory was formulated as an expansion in a parameter we called g_s, the string coupling constant. It is clear from that formulation that, when g_s is large, the later terms in the sum will contribute more. These terms are very difficult to calculate. In other words, when g_s is large, we don't know our string theory very well.Suppose now that we had string theory A with string coupling constant g_s^A, and string theory B with string coupling constant g_s^B. And suppose we could find a map between string theory A and string theory B such that g_s^B is mapped to 1/g_s^A. It is now clear that as g_s^A becomes large, g_s^B becomes small. Therefore, once we loose control over our expansion in string theory A, we precisely have another description, string theory B, for which the expansion parameter g_s^B is small. That type of duality is known as S-duality, and once we have an S-duality between string theory A and B, we have control over both theories, whether their string coupling is large or small. S-duality is therefore a powerful tool to learn about string theories at large coupling.
Note that in this case we found a duality that links one string theory to another string theory. Actually, there are also instances of this phenomenon in the case of T-duality. In that case, string theory A on space X is equivalent to string theory B on space Y. But in both string theories the coupling would be weak. That is a crucial difference between S- and T-duality.