Welcome
Introduction
Links and Refs
Standard Model
Accelerators
Relativity
Nobel Prizes
String Theory
Unification
Extra dimensions
Sociology
Duality
Internet
Branes
Black holes
M-Theory
Reactions
Mail me

  III. General Relativity
The Standard Model chapter exhibited three of the four known forces in nature. The present chapter, on General Relativity, treats the fourth and final one. Thereby, we introduce the second pillar on which string theory rests. We explain why general relativity stands separate from the Standard Model, and after treating some of its main principles, we move on to explain the shortcomings of Relativity theory.

The heavy

The Standard Model describes the basic structure of matter. It explains the existence of atoms, molecules and large objects, and why objects do not pass through each other, and that we see and hear, for instance. It also describes the physical phenomena in particle accelerators to an impressively high precision, and still there is an obvious ingredient of our everyday lives that is lacking in the Standard Model.

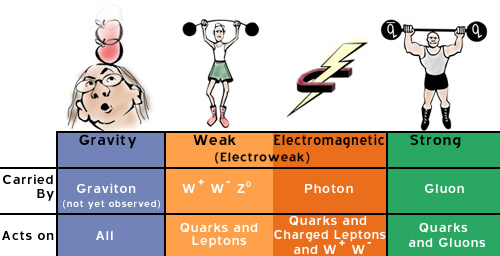
The Standard Model cannot explain the fact that an apple falls from a tree. It can describe the existence of the apple and of the tree, but the net force between them, including only the forces in the Standard Model, is zero. All electromagnetic, weak and strong forces cancel out. The force responsible for the apple hitting the ground, is the fourth force known to man, the gravitational force. That force is simply not part of the Standard Model. So, why did we not include it in the Standard Model ?

Most phenomena that we observe are either explained in terms of the Standard Model, or by General Relativity. The terrain where the quantum field theory of the Standard Model operates, is the terrain of small elementary particles, with tiny masses. General Relativity on the other hand, pertains to heavy objects that are usually so large that most of the forces predicted by the Standard Model just cancel out amongst the many particles that make up the heavy objects. (If they would not cancel out, the objects would rapidly aggregate into larger objects for which these forces would cancel out.) The Standard Model can attain incredible accuracy in experiments with elementary particles, because these particles are so light, and because the gravitational force is so weak as to have -- for now -- no measurable effect on accelerator experiments. That's why we could place the two theories in a separate chapter.

(Remember though that the special theory of relativity is incorporated in quantum field theories and is tested to a high precision in particle accelerators. Special relativity has large and measured effects on very fast elementary particles. The particles do not need to be heavy for these effects to be large. Hence we were forced to treat special relativity as part of the Standard Model, as we did. General Relativity is an entirely different matter, from this perspective.)

A dynamical arena

The theory of General Relativity then, was developed almost separately from the theory of quantum fields, and in a first approximation, we can start all over again and explain the phenomena associated to the fourth, gravitational force without having to refer to the previous chapters. We will have to pay for this schizophrenic attitude later though.

Before the theory of General Relativity was formulated, the arena in which all physical phenomena took place, was the spacetime in which we imagine to live in our everyday lives. We are used to think of being able to move a chair from one side of the kitchen to another, and imagine that the kitchen does not change. We attribute to space (the kitchen) an absolute property -- it does not change as we move objects around in it. Similarly, physicists used to think that spacetime did not vary while all kinds of physical phenomena (for instance movement) occurred. The everyday picture turns out to be false when looked at in more detail.

Before we demonstrate how our everyday intuition fails, we have to start out by getting a grip on the aspects of general relativity that we do know from our everyday lives. The theory describes the attraction of massive objects. Indeed, it describes the falling of the massive apple towards the very massive earth. It also describes the incredible tiny bit of movement of the earth towards the apple -- the movement is tiny not because the force on the earth is different from the force on the apple, but because the earth is so massive that is it more difficult to make it budge.

Similarly, the theory of general relativity describes the attraction of the earth by the even more massive sun, the attraction of the moon by the earth (and the attraction of the water in the sea by the moon), the attraction of our massive galaxy by other galaxies, of clusters of galaxies by other clusters of galaxies, and the attraction of light by such extremely massive objects like black holes. All of these phenomena are not too difficult to understand intuitively -- they are all mere large scale copies of the apple-earth example, where one has to keep in mind the relative masses of the objects involved in the attraction to get a good feel for how they will behave. Very massive objects exert a very strong attractive force. Very massive objects are difficult to move.

What is less intuitive is the mathematical description used to make this process of attraction more precise. It will turn out that the description involves new concepts, most importantly that the spacetime (kitchen) we imagined to be absolute, is not. The arena in which physical phenomena occur is dynamical. The kitchen is not as inert as we thought it was. The kitchen will in some sense be different (itself) whether the chair is in it, or not.

Mass and curvature

The way in which the mathematics describes the attractive force between two masses, is by describing spacetime to be curved around each massive object separately (whether a second body is present or not). The curved spacetime caused by one massive body, causes a second massive body in its vicinity not to fly in a straight line. The trajectory of the second massive body is bended towards the first massive body. Thus the net effect is that the second massive body is attracted towards the first massive body, and that is exactly what we observe. (We can exchange the first and second body in our reasoning, and it remains equally valid, but remember that the curvature caused by a massive object grows with its mass, and can be very small when the massive object is not very heavy. Thus the effect of the apple on spacetime is smaller than the effect of the earth on spacetime.)

Thus, we now imagine spacetime to be a dynamical arena, full of massive objects that make the (elastic, dynamic) fabric of spacetime curved, dented or rippled. And all of these objects follow bent trajectories in the mountain landscape thus created (by all bodies). This may sound like an elaborate way to describe a 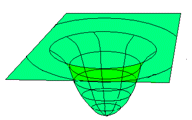simple attractive force. It is elaborate, but it turns out, in its details, to be an extremely accurate description of the strange trajectories of the planets, the moons, the comets, the stars, and the galaxies that we can see through our telescope. (Thus the space in the kitchen is bent around the chair when the chair is present, and it is not when the chair is not there. Of course, the main effect of the bending of the fabric of the kitchen is caused by the earth's presence. This is why plates will tend to fall to the floor of your kitchen (whether the chair is there or not). They will also be attracted to the chair, when it is present, but we do not observe this very tiny effect. Unfortunately.)

A weak force

Most importantly, the precise mathematical description of the attraction of massive bodies in General Relativity is more accurate than the Newtonian one, which did not take into account the dynamics of spacetime itself. The deflection angle of light rays of stars that pass right next to the sun, for instance, confirmed the theory of General Relativity. Only by taking into account the bending of spacetime itself could the precise angle be explained. (Try to find the story of the polar expedition that first measured this effect on the internet.)

When we combine the results of General Relativity with the well-known result of special relativity that energy is equal to mass, we get the powerful conclusion that actually anything with the slightest bit of energy changes the fabric of spacetime. It is only because the gravitational force is so weak that our environment still looks fairly stable. When we move a chair from one side of our kitchen to the other, the space in the kitchen is distorted. The kitchen does change, but only such a tiny little bit that we don't notice. The only circumstances in which we notice the gravitational force is when the build-up of mass is so big, that all the tiny forces on the separate massive constituents conspire to create a tangible net effect. This is the case when the whole mass of the earth pulls on an apple or a plate.

Quantum

Now that we understand the basics of both the Standard Model and General Relativity, we can ask some penetrating questions. First of all, General Relativity describes objects, whether large or small, as having a well-defined position, but that is in contradiction with the principles of Quantum Mechanics (QM1). Is there a simple resolution to that paradox ? Answer: No, definitely not a simple one. A more concrete question is: we learned that the forces of the Standard Model are transmitted by photons, vector bosons, or gluons, for the electromagnetic, the weak and the strong force respectively. Now that we have a fourth force, do we have another messenger particle ? Answer: We haven't observed it yet, but we already gave the particle a name: the graviton. We can predict several of its properties and are fiercely looking whether we can observe it. In what theory should we try to fit this graviton ? How penetrating can our theoretical questions be when we make use of both the Standard Model and General Relativity, and when do they become relevant for observation ? An ser: we do not know, although we're busy trying to provide you with an answer.

The Graviton

A tentative answer to these penetrating questions might be the following. There should be a messenger particle, the graviton, and from its classical description in general relativity we can surmise it has spin 2. It is not a charged particle. (Note that it would be easy to observe otherwise.) There could be a quantum field theory that would describe the interactions of all elementary matter particles and messenger particles with the graviton. That is the most obvious unification of what we learned in the previous chapters. Unfortunately, after decades of efforts, nobody has made sense of such a quantum field theory of gravity. And there are good arguments that nobody ever will. Here we are faced with a hard question in contemporary theoretical physics. Can we formulate a good quantum theory of gravity that would unify the Quantum Mechanics of the Standard Model with the gravitational interactions described by classical General Relativity ? And, if it isn't a quantum field theory, what is it then ?

In common

The question we posed is not only a hard question in theoretical physics. Since it is a physical question, we can directly translate it into a question on experiments. There are circumstances in which only the large scale gravitional interactions are important, and there are circumstances in which only the interactions described in the Standard Model are important. These circumstances are the ones of our everyday lives, and even of the most intricate experiments hitherto performed. What will happen though, when both the gravitational force and the quantum-mechanical interactions of quantum field theory become important ? We begin to address all these questions in the next section. Many would argue that this is the most important question in contemporary physics -- all experts will agree that it is an important one.