Welcome
Introduction
Links and Refs
Standard Model
Accelerators
Relativity
Nobel Prizes
String Theory
Unification
Extra dimensions
Sociology
Duality
Internet
Branes
Black holes
M-Theory
Reactions
Mail me

IV. String Theory
Theory beyond experiment
Present day particle accelerators probe distances of about 0,000000000000001 meter (or foot). And there are compelling arguments for the fact that gravity certainly will become important once the accelerators probe distances of about 0,00000000000000000000000000000000001 meter. In other words, we are a far way off from building an accelerator for which we are certain that we will need a unified theory that incorporates quantum field theory and general relativity. That does not mean there are no experiments at all that can guide us in formulating such a unified theory. In the cosmos, there are lots of natural phenomena that involve tremendous amounts of matter, or very densely packed elementary particles, or very high energy radiation or particles, and from looking at and exploring the sky, we might learn about the right properties of a unified theory. The biggest problem with this kind of experiment is that it is uncontrolled, and we can hardly ask for the high precision we might demand from careful laboratory experiments. We have to be careful in interpreting the clues we get from observing the sky, but we will nevertheless make an attempt to incorporate them in our unified theory, and we will treat some of the important celestial observations in the following.
Consistency
Given the lack of sufficient experimental data in the physical arena where both quantum field theory and general relativity become important, it might seems that there could be thousands of theories that incorporate both theories, and that there is no way to distinguish between them. That turns out not to be true, and it is one of the prime theoretical motivations for believing in string theory.One of the reasons why there is no plethora of theories unifying quantum mechanics and general relativity is straightforward to explain. They contradict each other. Indeed, general relativists work under the assumption that massive point like particles follow specified line like trajectories. We already know that this contradicts the inherent fuzziness of quantum mechanics. Massive point like particles are actually better interpreted as clouds of some extent, and there exists some uncertainty about their precise position or momentum. That contradiction in the basic assumptions of the theories proves difficult to get rid off. We will refer to a theory that resolves this contradiction as a theory of quantum gravity.
Given this contradiction, what do we expect a unified theory of general relativity and quantum field theory to look like ? The problem is quite straightforward to state. Firstly, a unified theory should reduce to the quantum field theory of the Standard Model precisely in those physical circumstances where the Standard Model describes physics accurately. Secondly, a unified theory should reduce to general relativity in precisely those physical circumstances where general relativity describes physics accurately. Thirdly, in those circumstances where we might have expected that both theories would apply, we need new basic principles to replace the old ones. In other words, the above contradiction already warns us that the basic principles of a unified theory will be drastically different from what we know.
Remedies
A unified theory that satisfies all the demands that we imposed on it above, has not been constructed so far, and only one attempt has come very close. First of all, it should be stated that several theories of quantum gravity have been constructed that resolved the contradiction above, but that do not satisfy the first of our criteria -- we will only be interested in theories of quantum gravity that do.The only attempt then that comes extremely close to satisfying all three criteria is called String Theory. In this chapter we will try to give the reader an idea of that the surprising basic principles are that the theory is based upon. But first of all we stress the importance of the fact that after decades of vigorous research by hundreds of theoretical physicists, we still haven't come up with a decent alternative for the theory of strings, that would also satisfy the reasonable criteria enumerated above. To almost all theorists, and many experimentalists, this is a compelling reason to take string theory seriously.
A principle
What are then the surprisingly new principles that string theory is based on ? Firstly, and most importantly, it replaces the basic principle of point like particles that underlied our intuition for quantum field theory and general relativity with the idea that the elementary excitations of our universe are not particles but strings. That is where string theory derives its name from. That new basic principle is the source of many new spectacular phenomena that are difficult to guess at first sight.What then, are these strings made off, one can wonder. They are made of nothing but little lines of energy, and when one tries to divide them up, they just form new little stretches of energy. There is no elementary constituent smaller than these little lines of energy. That is one surprising property that we have to keep in mind. A second elementary question is more easily dealt with: why don't we see these strings ? Because they are tiny. We know that they can be at most 0,000000000000001 meters wide, since otherwise we would have seen the little lines of energy in particle accelerators. But as long as they are smaller than that, they will appear to every microscope, the human eye, or a particle accelerator like point particles. Indeed, there width is smaller then the resolution of our screen (say), and they will only fill out a single dot. They look like points.
Actually, there are no objections at all to thinking of the elementary constituents of nature as string like objects. What do we gain from that first principle though ? That is not obvious from the start, but it will become clear as we go along. Let's first take a look at the theory of open loops, or open strings, and see what we learn from it.
Open strings
It turns out that a quantum mechanical theory of open string can be formulated, and that it automatically incorporates a lot of excitations that look like particles. One of those excitations is a vector particle that is exactly massless. That should sound familiar. Indeed, we encountered massless vector particles before. They were the key messengers we saw in our description of the Standard Model. In other words, the quantum mechanical formulation of a theory of open strings automatically incorporates one of the key ingredients of the Standard Model. Before we calculated the theory, we couldn't know this. It just turns out that we struck lucky. There's the first surprisingly good characteristic of string theory.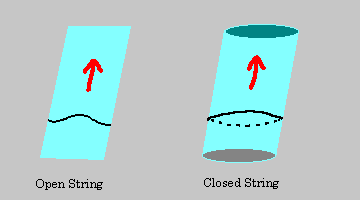
There turns out to be a problem though with open string theory. Indeed, open strings can merge into closed loops of energy, and these were not at first accounted for in our theory. It is as if we can make something that isn't in our theory in the first place. That is a problem. It leads to the conclusion that we not only need to accept open strings as our basic ingredients, but also closed loops of energy, closed strings.
Closed strings
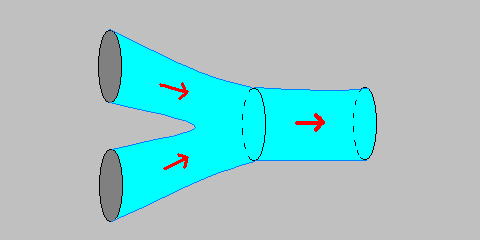
Now, a quantum mechanical theory of closed strings also incorporates a lot of massless particle like excitations. And again, there is one among them that is very special, and familiar. It is a massless spin 2 particle. Remember, that we didn't order this. But we get it anyway, and miraculously, it is exactly what we need to formulate the theory of General Relativity. We struck lucky again. It is the crucial second characteristic of string theory.
By merely studying the theory of open and closed strings, or string theory, in its quantum mechanical formulation, we got everything we needed to formulate a unified theory that incorporates the Standard Model and General Relativity. That doesn't mean we already have the unified theory, but it says we're on the right track. The irony in this development needs stressing perhaps. By making a crazy assumption about the elementary constituents of nature, and then carefully analyzing the theoretical (mathematical) consequences of that assumption, we got more than we dreamed we could ever obtain. We got more than enough motivation to delve deeper into the theory of strings.