Figure
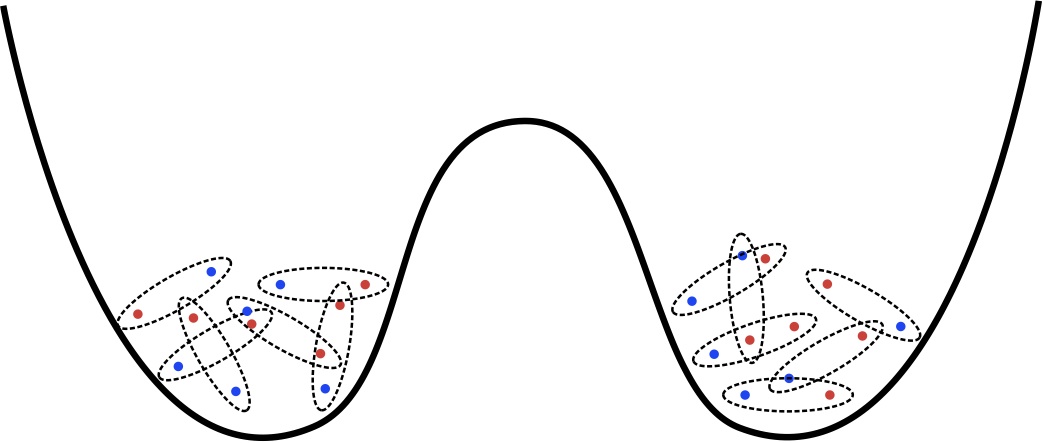
Two pair-condensed Fermi gases are prepared in a state with a well defined relative phase after splitting by a potential barrier. They subsequently evolve independently under the influence of interactions. This dynamics combined with the initial fluctuations in the atom numbers causes their phases to blur.