The liquid-gas phase
transition is well known in ordinary fluids and in our
everyday life. It has now attracted attention of the ultracold
atom community. It was indeed found by Quantum Monte Carlo
simulations, in the group of Werner Krauth at LPS of ENS, that
the unitary Bose gas (a gas with maximal, attractive
interactions) can have such a transition. The current attempts
of experimental realizations with ultracold atoms and
a Feshbach resonance in the lab, in the
group of Christophe Salomon at LKB, are hampered by too strong
atomic losses, due to three-body collisions.
A practical idea to get rid of the losses is to make the gas one-dimensional, using laser trapping in a matter-wave guide. The effective interaction in one dimension can then be made attractive using a Feshbach resonance, without inducing strong losses; this led in 2002 to the observation of a N-body bound state, by the group of Christophe Salomon, but totally out of thermal equilibrium. This N-body bound state is the quantum equivalent of the bright-soliton solution of the one-dimensional non-linear Schrödinger equation, and it is after all a liquid phase! It is unclear however what would happen at thermal equilibrium in a box, since there is no first order phase transition in one dimension, due to a celebrated argument by Lev Landau (see e.g. Imry and Scalapino, 1974).
The analytical solution of the N-boson problem in one dimension, with attractive Dirac delta function interactions, remains formidable in a box, even if it is integrable by the Bethe ansatz. Starting from the solution that we obtained in free space in 1997, we were able to construct a simplified model on microscopic grounds, in the limiting case where the box length is much larger than the diameter of a dimer and where the system is highly non-degenerate. Numerical exploration of this model suggests that there is a first-order phase transition from a quasi-monoatomic gaseous phase to an almost fully liquid phase (an almost undissociated N-body bound state), see figure. In the thermodynamic limit, we have shown analytically that there is indeed a liquid-gas transition, even if one includes arbitrary fragmentations of the liquid phase or arbitrary aggregations of atoms into n-mers in the gaseous phase, and we predict a transition width scaling as O(1/N). This paves the way to an experimental realization with ultracold atoms, which would be a premiere.
In reality, Landau's argument did not really exclude a liquid-gas transition in our system, because one of its key hypotheses, the extensivity of the liquid phase, is here not fulfilled, since the energy of the ground N-mer grows more rapidly than the number N of particles. One only had to think of it.
Figure :
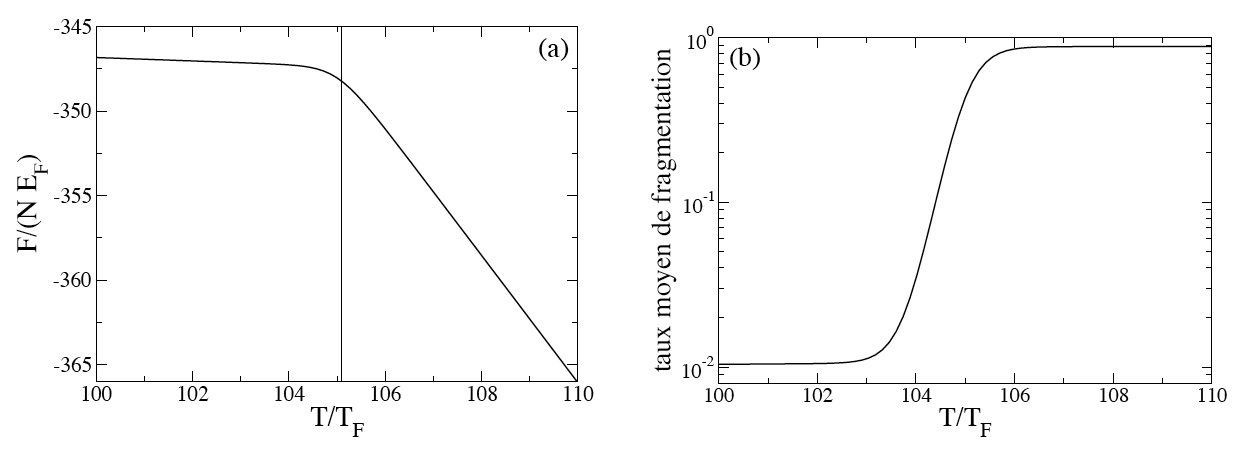
(a) For a one-dimensional system of N = 100 bosons with attractive interaction,
the change of slope of the free energy F as a function of temperature T suggests that
there is latent heat and thus a first-order phase
transition. (b) The abrupt change of the fragmentation
rate (from a value close to 1/N
to a value close to one) suggests that this is a liquid-gas
transition. What we call the fragmentation rate is the number of
fragments (atoms, dimers, ..., N-mer)
divided by the number of particles N, and EF=kBTF is the Fermi energy of a fictitious gas
of N fermions
with the same mass as the bosons. The length of the box is 100
times the diameter of a dimer.
Publication : "A liquid-gas transition for bosons with attractive interaction in one dimension", Christopher Herzog (YITP, Stony Brook, USA), Maxim Olshanii (UMB, Boston, USA), Yvan Castin (LKB-ENS), Comptes rendus Physique 15, 285 (2014) [in french] and HAL [in english and in french]
A practical idea to get rid of the losses is to make the gas one-dimensional, using laser trapping in a matter-wave guide. The effective interaction in one dimension can then be made attractive using a Feshbach resonance, without inducing strong losses; this led in 2002 to the observation of a N-body bound state, by the group of Christophe Salomon, but totally out of thermal equilibrium. This N-body bound state is the quantum equivalent of the bright-soliton solution of the one-dimensional non-linear Schrödinger equation, and it is after all a liquid phase! It is unclear however what would happen at thermal equilibrium in a box, since there is no first order phase transition in one dimension, due to a celebrated argument by Lev Landau (see e.g. Imry and Scalapino, 1974).
The analytical solution of the N-boson problem in one dimension, with attractive Dirac delta function interactions, remains formidable in a box, even if it is integrable by the Bethe ansatz. Starting from the solution that we obtained in free space in 1997, we were able to construct a simplified model on microscopic grounds, in the limiting case where the box length is much larger than the diameter of a dimer and where the system is highly non-degenerate. Numerical exploration of this model suggests that there is a first-order phase transition from a quasi-monoatomic gaseous phase to an almost fully liquid phase (an almost undissociated N-body bound state), see figure. In the thermodynamic limit, we have shown analytically that there is indeed a liquid-gas transition, even if one includes arbitrary fragmentations of the liquid phase or arbitrary aggregations of atoms into n-mers in the gaseous phase, and we predict a transition width scaling as O(1/N). This paves the way to an experimental realization with ultracold atoms, which would be a premiere.
In reality, Landau's argument did not really exclude a liquid-gas transition in our system, because one of its key hypotheses, the extensivity of the liquid phase, is here not fulfilled, since the energy of the ground N-mer grows more rapidly than the number N of particles. One only had to think of it.
Figure :

Publication : "A liquid-gas transition for bosons with attractive interaction in one dimension", Christopher Herzog (YITP, Stony Brook, USA), Maxim Olshanii (UMB, Boston, USA), Yvan Castin (LKB-ENS), Comptes rendus Physique 15, 285 (2014) [in french] and HAL [in english and in french]