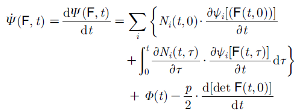ResearchClick on the articles to read more. |
|
||
|
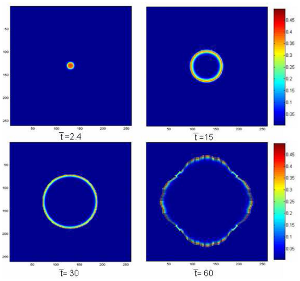
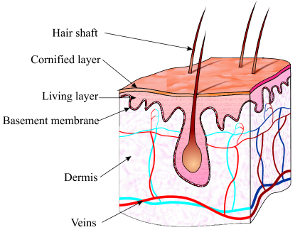
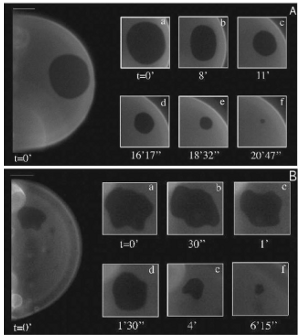
Skin tumour modeling Skin cancers are the most commonly observed form of cancerous lesions. Among them, melanoma is disproportionately lethal despite its relatively low incidence and its po- tential for cure in the early stages. The aim of this work is to understand the first steps in the development of melanoma, when they are confined within the epidermis. In this respect, we have developed in our group several models to describe the radial growth phase of cutaneous melanoma. The development of a ring of highly proliferative cells at the periphery of the tumor is responsible for the generation of non-trivial shape, a critical element of the clinical diagnosis. |
|||
|
Biomechanics and animal morphogenesis. The recent development of continuum-based theories for nonlinear, heterogeneous and active materials has allowed the description of the deformations and growth of living animal tissues. Using those theoretical tools, we have developed in our group a research activity that aim at describing major morphogenetic events, such as the embryogenesis of C.Elegans. We have shown that molecular motors activity can account for the elongation of the C.Elegans embryo during its early development. On a different ground, careful modeling of the microstruture of filamentous biological bodies has allowed to predict the complex (hysteretic) behavior of tendons and ligaments. The proposed models will serve as strarting points for more detailed studies on different systems, and may have applications in medecine or bioengineering. |
|||
|
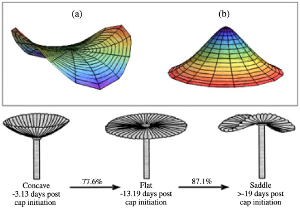
Vegetal morphogenesis. In opposition with animal tissues that dissipate energy, vegetal tissues are known to behave elastically under a broad range of experimental conditions. In order to accurately model some of the structures commonly observed in plants, leaves and petals, we have developed a model describing the growth of thin elastic sheets. The main result of this study is that growth induces preferential curvatures (mean and Gaussian) on the neutral surface of the sample. However, a surface with prescribed curvatures might no be physically accessible and residual elastic stresses are generated, which in turn deform the body. This model has been applied to different systems, such as algae or grass blades. |
|||
|
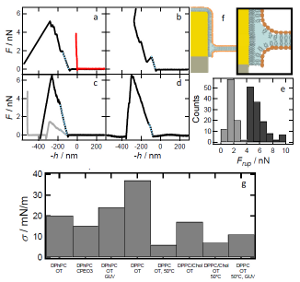
Instability in swelling hydrogel. The high level of complexity involved with biological tissues has led researchers to look for easily monitorable experimental substitutes in order to understand their mechanical properties. Hydrogels, which are polymeric substance with a high content of water and an ability to grow have been found to behave quite similarly to biological tissues. In this work, we have highlighted the main differences between the growth of living tissues with the swelling of gels. In addition we have shown that nonlinear elasticity can explain the formation of the highly singular structures observed at the surface of hydrogels. |
|||
|
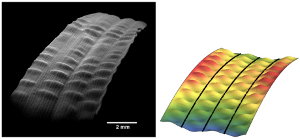
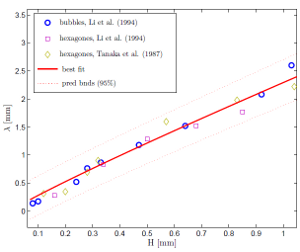
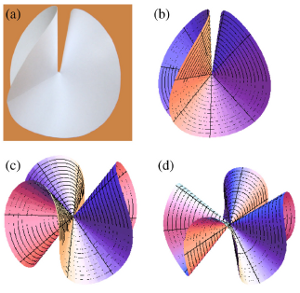
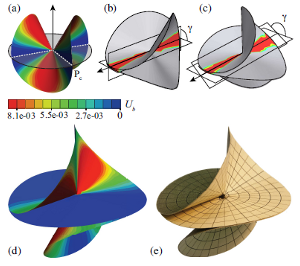
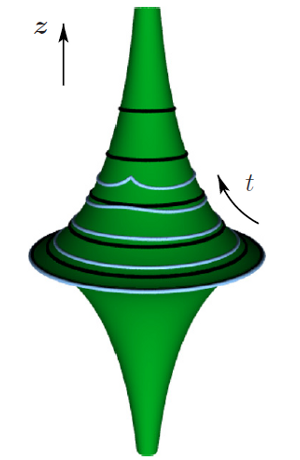
Elastic singularities Thin elastic samples possess an intriguing capacity of stocking energy when subject to an external force. If possible, they will preferentially bend, without stretching. When this is not possible, some stretching is necessary. However, in some situation, stretching is focused on very small portions of the system, such as lines or points, forming highly energetic structures, folds and cones. Those regions are linked together by large area of unstretched material. Following the seminal work of Ben Amar and Pomeau, the group has focused on the interplay between growth and those singular structures. |
|||
|
Biological membranes. |
|||
|
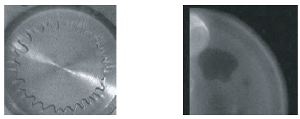
Instability in this liquid crystal films. Recent experiments in the group of Anne-Marie Cazabat (LPS, ENS) demonstrated that thin nematic films, spread on liquid substrates, exhibit a long-wavelength periodically deformed state (stripes) up to the thickness of 20 nm. The formation of stripes in thin nematic films can be attributed to the response of the system to the antagonistic boundary conditions. Although being extensively studied in the last two decades, these new observations cannot be explained completely by the existing theories. To get some theoretical insight on the experimental findings, we reconsider the onset of stripe instability in ultra-thin nematic films in the framework of the continuum theory of liquid crystals. |
|||
|
Faraday instability. |
|||
|
| ||
| -- last update: March 24 2016 |

|
|
|
| ||